Home  ›  How Do You Know When Its Single Slit or Double Slit on Laser

How Do You Know When Its Single Slit or Double Slit on Laser

Written By Friday, March 11, 2022 Add Comment Edit

Diffraction

25 Single-Slit Diffraction

Learning Objectives

By the cease of this department, you lot will be able to:

  • Explain the phenomenon of diffraction and the conditions under which information technology is observed
  • Describe diffraction through a single slit

After passing through a narrow discontinuity (opening), a wave propagating in a specific direction tends to spread out. For example, sound waves that enter a room through an open door can be heard even if the listener is in a part of the room where the geometry of ray propagation dictates that there should only be silence. Similarly, ocean waves passing through an opening in a breakwater can spread throughout the bay inside. ((Effigy)). The spreading and angle of sound and body of water waves are 2 examples of diffraction, which is the angle of a moving ridge effectually the edges of an opening or an obstacle—a phenomenon exhibited by all types of waves.

Because of the diffraction of waves, ocean waves inbound through an opening in a breakwater tin spread throughout the bay. (credit: modification of map data from Google World)

Photograph showing the top view of a breakwater near a beach. There is an opening in the breakwater allowing waves to enter.

The diffraction of sound waves is apparent to u.s.a. because wavelengths in the audible region are approximately the aforementioned size as the objects they encounter, a condition that must be satisfied if diffraction effects are to be observed hands. Since the wavelengths of visible light range from approximately 390 to 770 nm, most objects do not diffract lite significantly. However, situations practice occur in which apertures are pocket-size enough that the diffraction of calorie-free is appreciable. For example, if y'all place your middle and index fingers close together and expect through the opening at a low-cal bulb, y'all tin run across a rather clear diffraction blueprint, consisting of light and dark lines running parallel to your fingers.

Diffraction through a Single Slit

Calorie-free passing through a single slit forms a diffraction design somewhat unlike from those formed past double slits or diffraction gratings, which nosotros discussed in the affiliate on interference. (Figure) shows a single-slit diffraction design. Annotation that the central maximum is larger than maxima on either side and that the intensity decreases rapidly on either side. In contrast, a diffraction grating (Diffraction Gratings) produces evenly spaced lines that dim slowly on either side of the center.

Single-slit diffraction pattern. (a) Monochromatic light passing through a unmarried slit has a fundamental maximum and many smaller and dimmer maxima on either side. The cardinal maximum is six times higher than shown. (b) The diagram shows the bright central maximum, and the dimmer and thinner maxima on either side.

Figure a shows a vertical line on the left side. This has a gap of length D. A vertical wave is shown on the right. The wave has a high crest in the center, corresponding to the slit. The wave attenuates on both top and bottom. An arrow along the central crest of the wave, pointing towards the slit is labeled intensity. Figure b shows a strip with horizontally marked light and dark lines. The central line, corresponding to the slit is the brightest.

The analysis of unmarried-slit diffraction is illustrated in (Figure). Here, the light arrives at the slit, illuminating it uniformly and is in phase across its width. We then consider light propagating onwards from different parts of the same slit. According to Huygens'southward principle, every part of the moving ridge front in the slit emits wavelets, every bit we discussed in The Nature of Lite. These are similar rays that start out in phase and caput in all directions. (Each ray is perpendicular to the wave front of a wavelet.) Assuming the screen is very far away compared with the size of the slit, rays heading toward a common destination are nearly parallel. When they travel straight ahead, as in function (a) of the figure, they remain in phase, and we observe a primal maximum. Nevertheless, when rays travel at an angle \theta relative to the original management of the axle, each ray travels a dissimilar distance to a common location, and they tin can arrive in or out of phase. In office (b), the ray from the lesser travels a altitude of ane wavelength \lambda farther than the ray from the top. Thus, a ray from the center travels a distance \lambda \text{/}2 less than the one at the bottom edge of the slit, arrives out of phase, and interferes destructively. A ray from slightly in a higher place the center and one from slightly to a higher place the bottom also cancel one some other. In fact, each ray from the slit interferes destructively with some other ray. In other words, a pair-wise cancellation of all rays results in a dark minimum in intensity at this angle. By symmetry, some other minimum occurs at the same angle to the right of the incident direction (toward the bottom of the figure) of the low-cal.

Lite passing through a single slit is diffracted in all directions and may interfere constructively or destructively, depending on the angle. The difference in path length for rays from either side of the slit is seen to be D sin \theta.

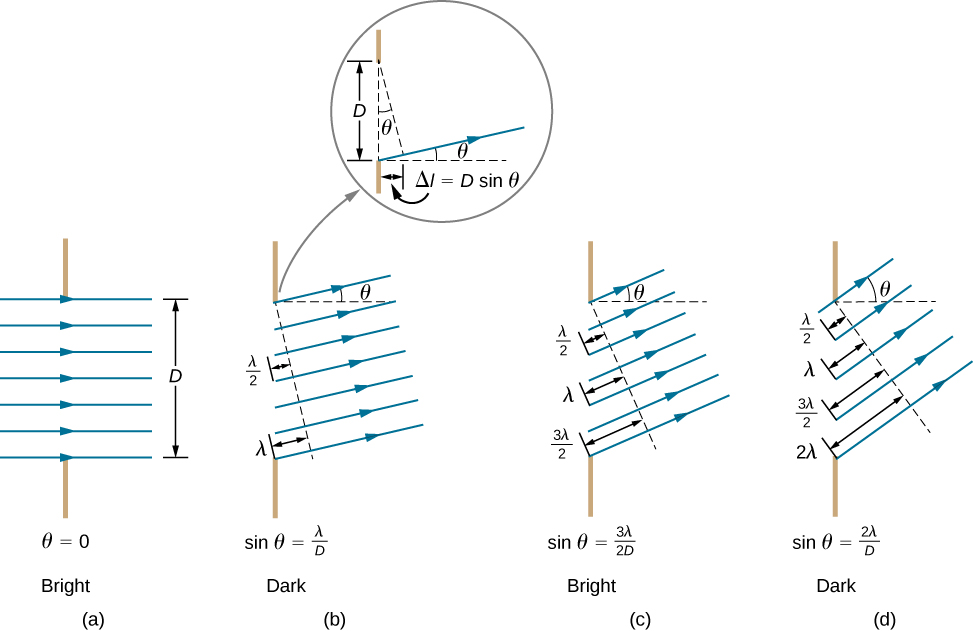
Figure a shows horizontal rays passing from left to right through a vertical slit of length D. This is labeled theta equal to zero, bright. Figure b shows rays passing through the slit at an angle theta to the horizontal. This is labeled sine theta equal to lambda by D, dark. A dotted line perpendicular to the rays touches the top of the slit. Its perpendicular distance from the bottom of the slit is lambda and that from the center of the slit is lambda by 2. A separate view shows the dotted line being at an angle theta to the vertical. It intersects the ray starting from the bottom of the slit at a particular point. The horizontal distance of this point from the slit is delta l equal to D sine theta. Figure c shows rays passing through the slit at an angle theta to the horizontal. This is labeled sine theta equal to 3 lambda by 2 D, bright. A dotted line perpendicular to the rays touches the top of the slit. Its perpendicular distance from the bottom of the slit is 3 lambda by 2. Figure d shows rays passing through the slit at an angle theta to the horizontal. This is labeled sine theta equal to 2 lambda by D, dark. A dotted line perpendicular to the rays touches the top of the slit. Its perpendicular distance from the bottom of the slit is 2 lambda.

At the larger angle shown in part (c), the path lengths differ by 3\text{λ}\text{/}2 for rays from the top and bottom of the slit. One ray travels a altitude \lambda different from the ray from the bottom and arrives in stage, interfering constructively. Two rays, each from slightly above those two, also add constructively. Virtually rays from the slit have another ray to interfere with constructively, and a maximum in intensity occurs at this angle. However, non all rays interfere constructively for this situation, so the maximum is not equally intense as the key maximum. Finally, in function (d), the angle shown is big enough to produce a second minimum. As seen in the effigy, the departure in path length for rays from either side of the slit is D sin \theta, and nosotros see that a destructive minimum is obtained when this distance is an integral multiple of the wavelength.

Thus, to obtain destructive interference for a single slit,

D\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta =m\lambda ,\phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}m=±1,±2,±3,...\left(\text{destructive}\right),

where D is the slit width, \text{λ} is the low-cal's wavelength, \theta is the angle relative to the original direction of the light, and k is the club of the minimum. (Figure) shows a graph of intensity for single-slit interference, and it is apparent that the maxima on either side of the central maximum are much less intense and not as wide. This effect is explored in Double-Slit Diffraction.

A graph of single-slit diffraction intensity showing the cardinal maximum to be wider and much more intense than those to the sides. In fact, the central maximum is six times higher than shown here.

Figure shows a graph of intensity versus sine theta. The intensity is maximum at sine theta equal to 0. There are smaller wave crests to either side of this, at sine theta equal to minus 2 lambda D, minus lambda D, lambda D, 2 lambda D and so on.

Calculating Single-Slit Diffraction Visible lite of wavelength 550 nm falls on a single slit and produces its second diffraction minimum at an angle of 45.0\text{°} relative to the incident direction of the light, as in (Figure). (a) What is the width of the slit? (b) At what angle is the first minimum produced?

In this example, nosotros analyze a graph of the single-slit diffraction pattern.

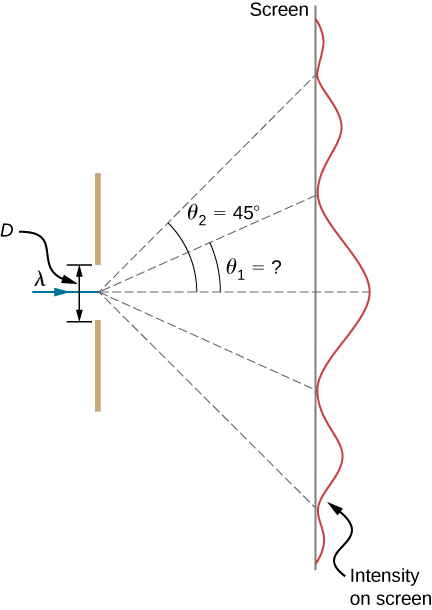
Figure shows a vertical line on the left. This has a slit in the middle, of length D. A ray labeled lambda passes horizontally through the slit. This splits into 5 dotted lines that fall on a screen. The screen is shown as a vertical line. Of the five dotted lines, two make angles theta 1 and theta 2 with the horizontal. Theta 2 is 45 degrees. Theta 1 is smaller than theta 2 and is unknown. Intensity on the screen is shown as a vertical wave. The crest at the center, where a horizontal dotted line from the center of the slit falls on the screen, is the largest. The wave attenuates at the top and bottom. The remaining four dotted lines correspond to troughs in the wave.

Strategy From the given information, and assuming the screen is far away from the slit, we can use the equation D\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta =m\lambda first to find D, and once again to find the angle for the first minimum {\theta }_{1}.

Solution

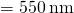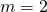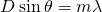  1. We are given that \text{λ}=550\phantom{\rule{0.2em}{0ex}}\text{nm}, m=2, and {\theta }_{2}=45.0\text{°}. Solving the equation D\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta =m\lambda for D and substituting known values gives

    D=\frac{m\lambda }{\text{sin}\phantom{\rule{0.2em}{0ex}}{\theta }_{2}}=\frac{2\left(550\phantom{\rule{0.2em}{0ex}}\text{nm}\right)}{\text{sin}\phantom{\rule{0.2em}{0ex}}45.0\text{°}}=\frac{1100\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{m}}{0.707}=1.56\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{m}.

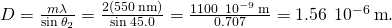
  2. Solving the equation 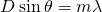D\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta =m\lambda for \text{sin}\phantom{\rule{0.2em}{0ex}}{\theta }_{1} and substituting the known values gives

    \text{sin}\phantom{\rule{0.2em}{0ex}}{\theta }_{1}=\frac{m\lambda }{D}=\frac{1\left(550\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{m}\right)}{1.56\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{m}}.


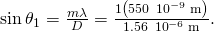
    Thus the angle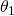 {\theta }_{1} is

    {\theta }_{1}={\text{sin}}^{-1}0.354=20.7\text{°}.

Significance Nosotros see that the slit is narrow (it is only a few times greater than the wavelength of light). This is consistent with the fact that light must interact with an object comparable in size to its wavelength in social club to exhibit pregnant wave effects such equally this single-slit diffraction pattern. We likewise run across that the key maximum extends 20.7\text{°} on either side of the original beam, for a width of nigh 41\text{°}. The angle between the starting time and 2d minima is merely about 24\text{°} \left(45.0\text{°}-20.7\text{°}\right). Thus, the second maximum is just nigh half as wide as the fundamental maximum.

Cheque Your Understanding Suppose the slit width in (Figure) is increased to 1.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{m}. What are the new angular positions for the outset, 2nd, and tertiary minima? Would a 4th minimum be?

17.8\text{°}, 37.7\text{°}, 66.4\text{°}; no

Summary

  • Diffraction can send a wave around the edges of an opening or other obstacle.
  • A single slit produces an interference pattern characterized by a broad central maximum with narrower and dimmer maxima to the sides.

Conceptual Questions

As the width of the slit producing a single-slit diffraction pattern is reduced, how will the diffraction pattern produced change?

The diffraction pattern becomes wider.

Compare interference and diffraction.

If you and a friend are on contrary sides of a loma, you tin can communicate with walkie-talkies only non with flashlights. Explain.

Walkie-talkies use radio waves whose wavelengths are comparable to the size of the hill and are thus able to diffract around the colina. Visible wavelengths of the flashlight travel as rays at this size scale.

What happens to the diffraction blueprint of a single slit when the entire optical apparatus is immersed in water?

In our written report of diffraction by a unmarried slit, we assume that the length of the slit is much larger than the width. What happens to the diffraction pattern if these 2 dimensions were comparable?

The diffraction design becomes 2-dimensional, with main fringes, which are at present spots, running in perpendicular directions and fainter spots in intermediate directions.

A rectangular slit is twice equally wide every bit it is high. Is the fundamental diffraction peak wider in the vertical management or in the horizontal direction?

Issues

(a) At what angle is the first minimum for 550-nm light falling on a single slit of width 1.00\mu \text{m} ? (b) Will in that location be a 2nd minimum?

a. 33.4\text{°}; b. no

(a) Calculate the angle at which a 2.00\text{-}\mu \text{m}-wide slit produces its first minimum for 410-nm violet lite. (b) Where is the commencement minimum for 700-nm red light?

(a) How wide is a single slit that produces its first minimum for 633-nm calorie-free at an bending of 28.0\text{°} ? (b) At what bending will the second minimum be?

a. 1.35\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{m}; b. 69.9\text{°}

(a) What is the width of a single slit that produces its first minimum at 60.0\text{°} for 600-nm light? (b) Find the wavelength of light that has its outset minimum at 62.0\text{°}.

Find the wavelength of light that has its tertiary minimum at an angle of 48.6\text{°} when information technology falls on a single slit of width 3.00\mu \text{m}.

750 nm

(a) Sodium vapor light averaging 589 nm in wavelength falls on a unmarried slit of width 7.50\mu \text{m}. At what bending does it produces its second minimum? (b) What is the highest-gild minimum produced?

Consider a single-slit diffraction pattern for \lambda =589\phantom{\rule{0.2em}{0ex}}\text{nm}, projected on a screen that is ane.00 m from a slit of width 0.25 mm. How far from the heart of the pattern are the centers of the showtime and 2d dark fringes?

2.iv mm, 4.7 mm

(a) Find the angle between the first minima for the two sodium vapor lines, which take wavelengths of 589.1 and 589.6 nm, when they fall upon a unmarried slit of width 2.00\mu \text{m}. (b) What is the distance between these minima if the diffraction blueprint falls on a screen one.00 m from the slit? (c) Hash out the ease or difficulty of measuring such a distance.

(a) If a unmarried slit produces a beginning minimum at 14.5\text{°}, at what angle is the second-society minimum? (b) What is the angle of the third-lodge minimum? (c) Is there a 4th-order minimum? (d) Use your answers to illustrate how the angular width of the central maximum is about twice the angular width of the next maximum (which is the bending between the first and 2nd minima).

If the separation between the first and the 2nd minima of a single-slit diffraction blueprint is 6.0 mm, what is the altitude between the screen and the slit? The light wavelength is 500 nm and the slit width is 0.16 mm.

1.92 m

A water intermission at the entrance to a harbor consists of a rock barrier with a 50.0-m-wide opening. Sea waves of 20.0-m wavelength approach the opening direct on. At what angles to the incident direction are the boats inside the harbor nearly protected confronting wave activeness?

An aircraft maintenance technician walks past a alpine hangar door that acts like a single slit for sound entering the hangar. Outside the door, on a line perpendicular to the opening in the door, a jet engine makes a 600-Hz sound. At what bending with the door will the technician observe the commencement minimum in sound intensity if the vertical opening is 0.800 m wide and the speed of sound is 340 yard/s?

45.1\text{°}

Glossary

destructive interference for a unmarried slit
occurs when the width of the slit is comparable to the wavelength of lite illuminating it
diffraction
bending of a wave around the edges of an opening or an obstacle

davisyouldon.blogspot.com

Source: https://opentextbc.ca/universityphysicsv3openstax/chapter/single-slit-diffraction/

0 Response to "How Do You Know When Its Single Slit or Double Slit on Laser"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel